A computational geometric perspective on the elegant phenomenon behind GPT like, BERT like large language models and what makes them so powerful.

The neural net architecture which changed the course of the field of machine learning (and might soon change tech industry itself), the transformers, can be quite intimidating at first glance. In this work, we will unravel the mysteries behind transformers by looking at it from a computational geometric perspective. On our journey, we will discover that contextualizing words, sentences and concepts, is the magic that lets LLMs learn what they learn. The term “Auto-contextualization”, refers to choosing a more appropriate term for the “attention mechanism” and is not proposing a change in the transformer architecture. The novelty here is to give a computational geometric perspective and strengthen the theory behind large language models.

The Power of LLMs

Lets start by asking the most famous LLM of today, a question.

Its very hard to argue that the answer doesn’t make any sense or that it is very simplistic. We could even do some research and find that the answer, although somewhat too broad, covers the spectrum of answers that we can find about language and human thought.

The aim of this write up is to give a computational geometric perspective, and show that an elegant phenomenon called Auto-contextualization is the reason behind the power of LLMs. And so, there is a lot of details that I have intentionally left out. For example, this don’t cover layer norm, drop-outs, multi-head attention, back-propagation, positional encoding, training long sequences, decoder-only architectures, beam search, tokenization, etc.

Masked Language Modeling

One of the other major breakthroughs of the last decade is the masked language modeling. Masked language modeling is a very simple technique to train neural networks to understand language. It works by masking parts of a sentence and asking the neural network to guess what could have appeared in the masked regions of the sentence. As with any other machine learning algorithm, the neural network is adjusted based on how correctly it guessed the masked region. This is done by an algorithm called the back-propagation, which is a very simple, yet extremely powerful technique widely used in training neural network models with complex architectures. Its a way to back-propagate the error (the difference between an predicted value and the actual value) through the neural network reaching every learnable parameter (back-propagation only finds the gradient and we take a step in that direction).

For example, assume the following sentence was pulled from linguistic texts. We are going to use this to train the neural network. The word approximately is replaced with a symbol (or token): [MASK].

Language approximately [MASK] encodes thought.

Tokenization and Vectorization

But wait, we have a sentence, what do we mean by passing it through a neural network? This is done in 2 simple steps. As the first step, the sentence is partitioned into tokens, for simplicity, let us assume each word is a token. And so, for the English language, there could be 237,000 tokens, which is the total number of words in the Oxford dictionary. As the second step, each of these tokens is assigned a learnable vector, which keeps changing and improving as the neural network goes through the learning phase. Additionally, we use some special tokens like [START], [END], [MASK], etc., which will also be assigned a learnable vector. As hinted above, the back-propagation technique allows these vectors to change to the desired value during the course of the neural network training. When we start the neural network training, we start with random vectors for each of the tokens.

The vector dimensions range anywhere between 768 to 18,432(PaLM) for these LLMs. However, for our purpose of gaining geometric intuition we use 3 dimensional vectors.

Multiplying giant matrices to create “intelligence” or Auto-contextualization

The vectors created thus far undergo a linear transformation. For the uninitiated, a linear transformation is nothing but a multiplication by a matrix; it deforms a vector, scaling it, rotating it, and/or reflecting it onto a different vector space (it can be of a different dimension too).

This linear transformation matrix, lets call it V, is learnable and initialized randomly, and we’ll let the same back-propagation algorithm to change this matrix during training.

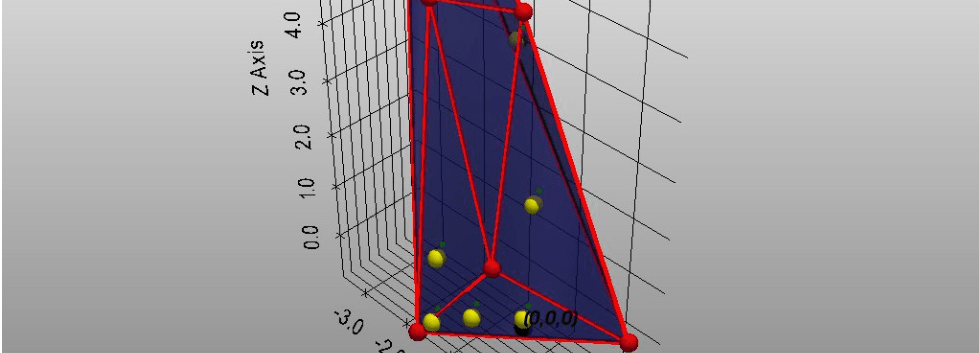
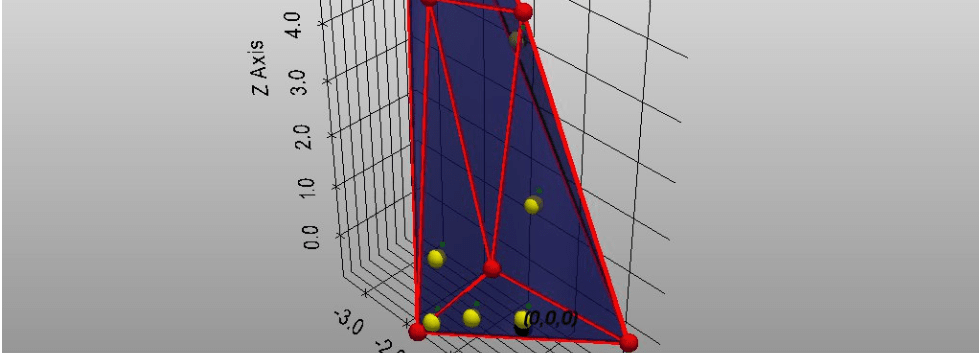
Lets find the convex polytope created by these transformed vectors.

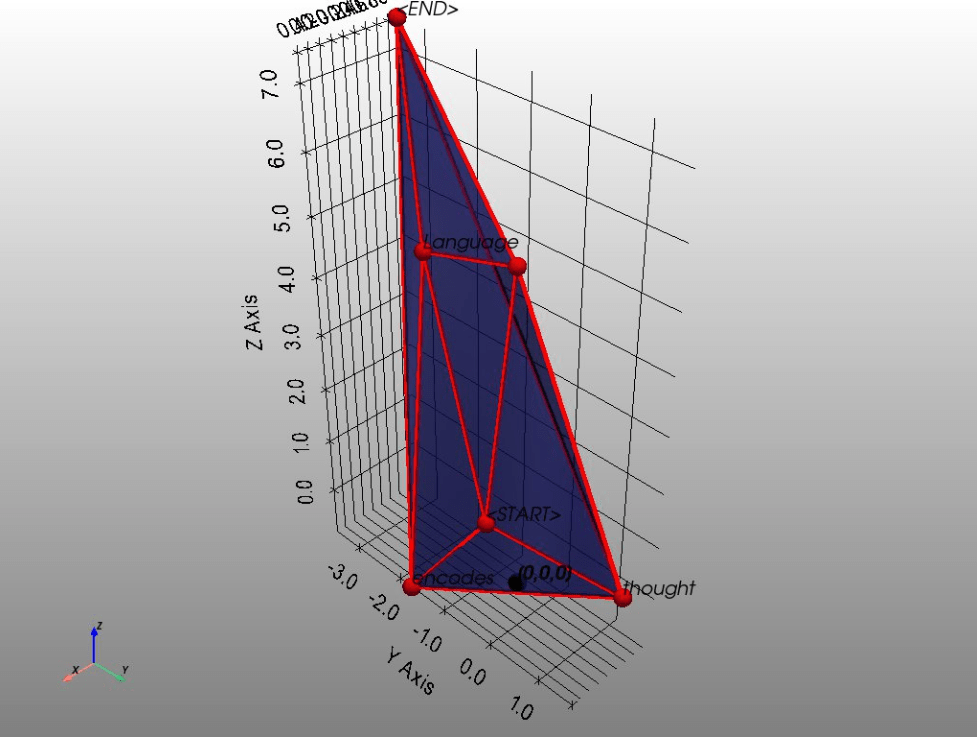
The vertices represent the words or tokens. If there was a systematic way to move these vertices around or to some interior point of the convex polytope, such that the word (or the sentence thus far) is contextualized even further, we could improve the representative power of the model. We can use convex analysis here to pick a point on the convex hull or another interior point inside the convex hull, as that is just the convex combination of the vertices (even if some of the vertices lie inside the convex hull).

Convex Combination

A convex combination of points on the surface of the convex hull, lies within the hull. But what about convex combination points on and inside the convex hull? This can be proved to be inside the convex hull too, and hence still within the relevant context.

Transformers are Auto-contextualizers

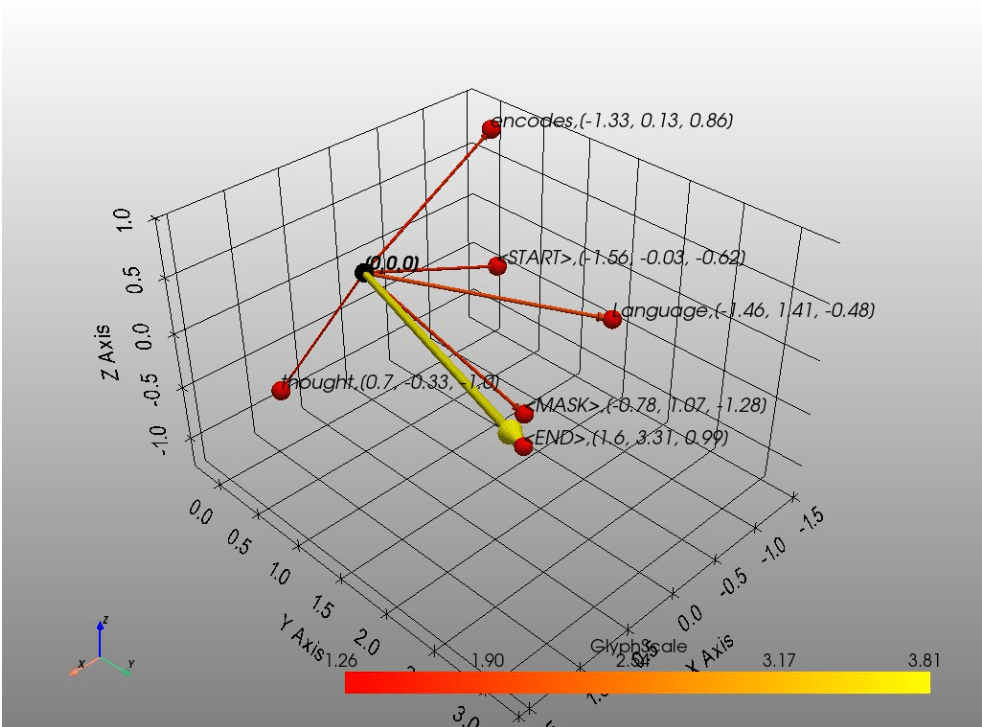
Auto-contextualization can be achieved if we can use the neural network to somehow learn how to contextualize words and sentences. That is to learn and find the convex combination itself. For Auto-contextualization, two new linear transformations are introduced. Two more matrices, Q and K, which will also be learned during neural network training.

Again, contextualization means moving a vertex (representing a token as a vector) around or inside the convex hull of the entire context polytope. This is demonstrated in the following write up.

The contextualized vector may pass through a few other transformations, before producing a probability distribution over all the tokens. If it assigns a higher probability to the word being masked, then the error is low. If the masked word was predicted wrongly, the error is back-propagated and the matrices are adjusted to reduce the error.

Context is a Polytope: Learns and Deforms

Usually, one layer of the auto-contextualizer is used for a good vector representation of the words or tokens. But the real-power of auto-contextualizers is unlocked when you stack these auto-contextualizers on top of each other. The network learns deeper contexts hidden in the language. A generative network of these stacked layers, like GPT, can see ingenious but are due to the power of auto-contextualizers.

The mini-batch acts as a regularizer and reduces noise during gradient descent. And as the training continues, these context polytopes deform: contort, shrivel or expand to better represent the context. The deeper layers take longer to learn, but nevertheless eventually learn higher concepts.

We end by asking two more questions to ChatGPT.

Conclusion

This write up showed that an elegant computational geometric view of the transformer architecture sheds light on how LLMs learn and where do they get such strong representational power. We also propose that auto-contextualization is a better terminology instead of the so-called “attention” mechanism. Auto-contextualization is a very powerful technique proved by the numerous applications of large language models are numerous and it has been shown that LLM’s can even pass academic tests. The computational geometric perspective is also meant to build intuition for the widely used transformer architecture. This work also sheds light on some concepts from convex analysis, which is already widely applicable in machine learning, and how it applies to auto-contextualization.